формула, цели и способы расчета, использование в финансовом анализе
В работе предприятия важно правильно управлять ресурсами. Главная цель – снизить себестоимость. При анализе состояния дел используется трудоемкость продукции, формула расчета которой основана на данных о затратах времени работников подразделений. Анализ результатов позволяет определить факторы, тормозящие развитие, оптимизировать количество работников и размеры издержек на заработную плату.
Понятие трудоемкости
Чтобы определить производительность, необходимо знать 2 показателя: трудоемкость и выработку. Трудоемкостью (интенсивность, трудозатраты) называются временные затраты, необходимые для выпуска единицы экономического продукта (товара, услуги, работы). Выработка одного работающего обратно пропорциональна трудоемкости, измеряемой в нормо-часах или человеко-часах.
В экономической теории выделено 5 видов трудозатрат:
- технологическая – зависит от временных затрат работников, занятых непосредственно на производстве
Понятие трудозатрат
- обслуживания производственных процессов – зависит от временных затрат вспомогательных работников
- производственная – зависит от временных затрат основных и вспомогательных (обслуживающих производство) работников
- управления производственными процессами – зависит от временных затрат офисных работников, охранников, обслуживающего персонала
- полная – включает в себя все временные затраты
Аналитики используют коэффициенты, разделенные по назначению. Рассчитываются 3 показателя трудозатрат:
- нормативных – время, отведенное на технологический процесс нормативами
- запланированных – запланированное время по изготовлению единицы экономического продукта
- фактических – время, потраченное на изготовление единицы продукции на практике
Трудоемкость рассчитывается для единицы продукции, отдельных операций, процесса, партий отдельных продуктов, валового продукта.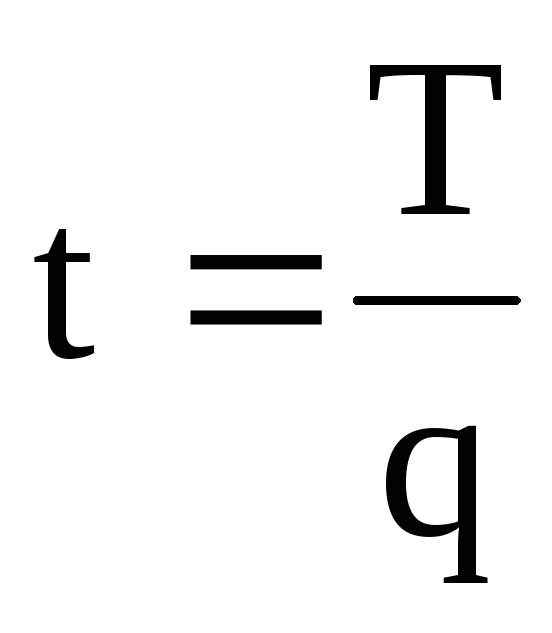 Этот коэффициент позволяет определить зависимость объема производства от затрат труда без учета изменений ассортимента и организационной структуры предприятия. Данные, полученные для отдельных участков, легко увязываются между собой и позволяют определить связь между производительностью и существующими резервами.
Этот коэффициент позволяет определить зависимость объема производства от затрат труда без учета изменений ассортимента и организационной структуры предприятия. Данные, полученные для отдельных участков, легко увязываются между собой и позволяют определить связь между производительностью и существующими резервами.
Аналитик определяет максимальный уровень производительности для конкретных условий, позволяющий оценить и оптимизировать работу предприятия.
Формула трудоемкости
Данный коэффициент рассчитывается при разработке производственных или бизнес-планов, анализируют эффективность используемой на предприятии рабочей силы, объема зарплат.
Величина зависит от:
- квалификации работников
- качества оборудования
- сложности технологического процесса
- уровня автоматизации
- условий труда
Формула:
Т=К/Q
- Т – трудоемкость единицы экономического продукта
Порядок расчета
- К – трудозатраты (время, потраченное на производство определенного объема продукции) или количество работников, которые участвуют в изготовлении определенного объема экономического продукта
- Q – количество единиц экономического продукта
Если вычисляются технологические затраты труда, то К – это количество работников, занятых непосредственно на производстве. Если требуется показатель для вспомогательного или управленческого персонала, К – время, потраченное этой категорией работников.
Производственные трудозатраты – сумма трудоемкости технологической и обслуживания. Полная интенсивность – сумма трудозатрат технологических, обслуживания и управления.
Нормативный показатель определяется по нормам выработки, времени, управления, обслуживания, численности работников. Чтобы разработать производственный или бизнес-план, сравнивают нормативные показатели с фактическими, чтобы определить, какие затраты следует снизить, чтобы достичь запланированных объемов производства.
Порядок расчета трудоемкости
Расчеты производятся последовательно:
- берутся табели учета рабочего времени, определяется количество работников в каждой категории и объем человеко-часов за какой-то период для отдельных участков, цехов, предприятия
- рассчитывается объем выпущенной продукции в единицах или стоимости
- значение коэффициента получается делением человеко-часов (количества работников) на единицы экономического продукта
Это фактический коэффициент трудовых издержек, который можно сравнить с нормативным или запланированным, чтобы выявить факторы, из-за которых возникли отклонения. Выводы аналитика позволяют повысить эффективность работы предприятия. Анализ за несколько периодов дает возможность определить динамику изменений, причины, которые их вызвали.
Цель бизнеса – повысить производительность путем снижения трудовых затрат. Если производится большой ассортимент продукции, важно рассчитать показатель для каждого вида. Полная трудоемкость может снижаться из-за изменения показателя для отдельного продукта или отдельного подразделения.
Производительность связана с издержками на зарплаты. На их уровень влияют экономические и организационные факторы, в том числе уровень управления. Анализ трудозатрат позволяет выявить недостатки в управлении, способствующие нерациональному использованию времени. Снижение коэффициента выгодно и для работников, так как является предпосылкой для увеличения заработной платы.
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Page not found — Сайт ecoorg!
Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.
- ГЛАВНАЯ
- КОНТАКТ
- БЛОГ
- НОВОСТИ
- О СЕБЕ
- МЕТОДИЧЕСКАЯ РАБОТА.
- СОДЕРЖАНИЕ ЗАНЯТИЙ
- Основной капитал
- Оборотный капитал предприятия
- Трудовые ресурсы и оплата труда.
- Планирование деятельности организации.
- Основы экономики
- «Экономика и управление
- Презентации
- Управление персоналом
- ПМ 03 Планирование и организация работы персонала подразделения
- Экзаменационные вопросы
- Вопросы к дифференцированному зачету
- Темы докладов и рефератов.
- Презентации
- Оперативно-производственное планирование
- Методы контроля использования сырья и материалов в производстве
- Практические занятия
- ПЗ №3, №4 Расчет норм труда и производительности труда
- ПЗ №5, № 6 Расчет трудоемкости продукции и численности рабочих.
- ПЗ №7 , № 8 Расчет заработной платы рабочих при повременной и сдельной оплате труда.
- ПЗ №9, № 10, №11 Расчет годового фонда зарплаты рабочих и ИТР
- №45, №46 Анализ эффективности использования оборотных средств.
- П/З № 47, №48 Анализ расхода сырья и материалов в производстве продукции.
- ПЗ №49, №50 Анализ себестоимости продукции.
- ПЗ № 51, №52 Анализ показателей прибыли предприятия.
- ПЗ №53, № 54 Анализ показателей рентабельности предприятия
- Контрольная работа
- Курсовая работа
- Учебная практика
- Вопросы к диплому
- Презентация к экономическому расчету диплома
- ПМ 03 Участие в организации производственной деятельности структурного подразделения.
- Практические занятия
- ПЗ №1. «Расчет длительности производственного цикла
- ПЗ №4 Расчет графика ППР оборудования
- ПЗ №5 Расчет трудоемкости ремонтных работ
- ПЗ №6 Расчет численности ремонтных рабочих.
- ПЗ № 7 Расчет годового фонда заработной платы ремонтных рабочих.

- ПЗ № 8 Расчет затрат на вспомогательные материалы и запчасти для ремонтных работ
- ПЗ №9 Расчет себестоимости ремонтов оборудования.
- ПЗ № 16 Расчет графика сменности в производстве.
- ПЗ № 29 Выбор структуры управления
- ПЗ № 31, 32 Методы управления
- ПЗ № 34 Управленческие решения
- ПЗ № 36, № 38, № 39 Должностная инструкция мастера по ремонту оборудования
- ПЗ №40 Мотивация труда
- ПЗ № 41 Анализ мотивации персонала по методу В.И. Герчикова
- ПЗ №43 Оценка стиля руководства
- ПЗ №44 Исследование основ власти по различным должностям
- ПЗ № 45, 46 Составление плана проведения делового совещания, беседы
- ПЗ № 47, 48 Трансакции
- ПЗ № 49, № 50, № 51 Конфликты
- ПЗ № 55 , № 53, № 54 Графические методы управления
- ПЗ № 56 Расчет потребности персонала по методу трудоемкости и нормам обслуживания
- ПЗ № 58, №59 Оценка текучести кадров, подготовка документов по найму на работу
- ПЗ №60, №61 Анализ деловых ситуаций, формирование коллектива
- Задание на самостоятельную работу.
- Экзаменационные вопросы
- Дифференцированный зачет
- Учебная практика
- Дополнительные материалы для отчета по учебной практике.
- Курсовая работа
- Производственная практика
- диплом
- МОИ СТАТЬИ
- РАБОТЫ СТУДЕНТОВ
Blog
Факторы роста производительности труда на предприятии (таблица)
Любое предприятие не может существовать без работников. Чтобы оценить производительность их труда, проводят анализ. Исследование помогает выявить резервы производительности труда и найти пути к повышению работоспособности сотрудников, что окажет благоприятное влияние на развитие компании, на ее финансовом благосостоянии в будущем.
Понятие производительности трудаВ экономической практике производительностью труда называют числовое выражение, которое характеризует степень выполнения трудовых обязанностей работников. Если говорить простыми словами, то производительность труда – это показатель работы сотрудников.
Если говорить простыми словами, то производительность труда – это показатель работы сотрудников.
Чтобы найти числовое выражение производительности труда, необходимо соотнести объем выполненных задач к затраченному времени на их исполнение.
Определяя производительность труда на одного сотрудника, обычно используют формулу, вычисление которой заключается в отношении между объемом произведенной продукции в единицах к среднему числу работников, участвующих в их производстве.
Определить производительность труда можно и другим способом. Для этого просто подсчитывают затраченное время на изготовление единицы изделия.
Виды производительности трудаЭкономисты различают два вида труда:
- совокупный.
Если первый вид подразумевает использование исключительно ручного труда, то совокупный заключается в совместной работе человека и машин.
Производительность труда также делится на фактическую, наличную и потенциальную. Все дело в том, что не все сотрудники на предприятии занимаются производством продукции, поэтому и показатель подразделяется на категории.
Фактическая производительность трудаРеальный показатель отражает фактическая производительность труда (далее ФПТ). Она рассчитывается по формуле:
ФПТ = Оп / Впп, где
Оп – объем изготовленных товаров за определенный промежуток времени в единицах;
Впп – время, затраченное на производство всей продукции, в часах, днях, неделях и т.д.
Пример 1. За 30 дней предприятие выпустило 8000 поддонов. Необходимо рассчитать производительность труда за сутки, за час.
Решение 1.
8000 / 30 = 266,67 – ФПТ за сутки;
8000 / (30 * 24) = 11,11 – ФПТ в час.
Наличная производительность трудаНаличная производительность труда (далее НПТ) отражает среднее возможное количество произведенной продукции за определенный промежуток, при условии использовании всех мощностей (рабочей силы, машин, станков).
То есть, НПТ показывает самое большее число товаров, которое может изготовить предприятие за некоторое время. НПТ рассчитывается по формуле:
НПТ = Опп / Впп, где
Опп – максимальный объем продукции, которое может произвести предприятие при использовании всех мощностей;
Впп – минимально возможное количество затраченного времени на изготовление товаров.
Потенциальная производительность трудаПотенциальная производительность труда (далее ППТ) отражает показатель выпуска продукции при использовании предприятием максимально усовершенствованных технологий. То есть, сколько фирма могла бы выпустить единиц товаров, если бы она обладала автоматизированной техникой нового поколения.
ППТ рассчитывается при определении целесообразности приобретения нового оборудования. После нахождения значения ППТ можно определить время окупаемости затрат на покупку новых технологий.
ППТ рассчитывается по формуле:
ППТ = МОп / МВ, где
МОп – максимально возможное число произведенной продукции при использовании новых технологий в единицах;
МВ – минимальное количество времени на изготовление товаров.
Резервы роста производительности труда (классификация)Анализ производительности труда проводят с целью выявления скрытых резервов. Их классифицируют на три крупные группы, а каждая из них еще раз делится на 2 подгруппы.
| Материально-технические резервы | Резервы совершенствования организации эффективного управления производством | Резервы социального назначения | |
| Классификация резервов ПТ в зависимости от возможности их применения | |||
| Использование запасов | Сокращение потерь | ||
| Резервы, классифицируемые по территориальному признаку | |||
| Региональные | Общегосударственные | ||
| Резервы, классифицируемые по отраслевому признаку | |||
| Межотраслевые | Внутрипроизводственные | ||
Для более точного понимания резервов роста ПТ, необходима их детальная расшифровка.
- Материально-технические резервы формируются в том случае, если на производстве не применяется высокотехнологичное оборудование, качественное сырье.
- Резервы совершенствования организации эффективного управления производством возникают при отсутствии контроля над производственным процессом, а также вертикальной системы управления.
- Резервы социального назначения образуются при недооценке личных качеств сотрудников фирмы. К этой же группе относят отсутствие мотивации работников, трудовой дисциплины.
- Резерв использования запасов предполагает задействование в производственном процессе машин, сырья, материалов, которые имеются в наличии на складе, но по какой-то причине, не применяемые ранее.
- Резерв сокращения потерь направлен на уменьшение выпуска бракованной продукции, рациональном использовании времени.
- Общегосударственные и региональные резервы связаны с территориальным расположением фирмы. В первом случае предприятию рекомендуется целесообразно использовать природные ресурсы и наладить взаимодействие с народом. Второй резерв подразумевает применение региональных возможностей.
- Межотраслевые резервы образуются за счет слияния, реорганизации либо разъединения цехов, а внутрипроизводственные призваны сократить затраты труда и оптимизировать издержки времени на производство продукции.
Факторы, оказывающие влияние на производительность трудаВажно! Использование резервов предполагает применение на производстве найденных в ходе анализа потенциально возможных путей улучшения производственного труда.
Показатель ПТ показывает точный объем выработанной продукции за определенный промежуток времени одним сотрудником либо бригадой.
ПТ является постоянно меняющимся показателем. Он напрямую зависит от объема приложенного труда и количества выработанной продукции. Именно поэтому основными факторами ПТ называют трудоемкость и выработку.
Использование факторов позволяет точно определить эффективность труда. Повышение ПТ скажется на увеличение объемов производства и сокращения расходов на выплату заработной платы.
Повышение ПТ скажется на увеличение объемов производства и сокращения расходов на выплату заработной платы.
На динамику ПТ оказывают влияние внутренние и внешние причины. К первым относят:
- приобретение нового оборудования;
- организация управления, смена персонала;
- обновление технологического процесса;
- мотивации сотрудников.
К внешним причинам роста ПТ относят экологические, политические и экономические факторы. То есть, динамика ПТ может произойти из-за особенностей погодных условий, каких-либо политических изменений и экономических сдвигов.
Показатели производительности труда на предприятииТрудоемкость и выработка являются основными факторами роста ПТ. Для оценки рассчитывают показатель каждого из них, который отражает рациональность использования трудовых ресурсов и продуктивность.
Выработка (понятие, формула расчета)Выработка показывает эффективность трудозатрат одного или нескольких работников за определенный промежуток времени. То есть, сколько единиц продукции произвел сотрудник за рабочий день, месяц и т.д.
Чтобы рассчитать показатель выработки за единицу времени, можно воспользоваться формулой:
ПВ = ОП / Кв, где
ПВ – показатель выработки;
ОП – объем готового продукта, изготовленного за промежуток времени;
Кв – количество затраченного времени сотрудниками на изготовление товаров.
Для расчета показателя выработки отрасли, цеха или всего предприятия на одного работника, используют формулу:
ПВ = ОП / Кр, где
Кр – количество работников, трудящихся на предприятии.
Трудоемкость (понятие, формула расчета)Обратный показатель выработки называют трудоемкостью. Он отражает количество затраченного временем сотрудника на производство одного товара.
Для расчета трудоемкости используют обратные формулы выработки:
ПТ = КВ / ОП, ПТ = Кр / ОП.
Однако, для получения более точной информации, с учетом простоев, используют улучшенную формулу:
ПТ = (ОП * (1 – К) / (Кв1 * Кр), где
ОП – объем готового продукта, изготовленного за промежуток времени;
К- коэффициент потерь;
Кв1 – количество затраченного времени сотрудником на изготовление товаров;
Кр – количество работников, трудящихся на предприятии.
В 2020 году для расчета роста производительности труда используют три метода: трудовой, натуральный и стоимостной.
Главное отличие способов вычисления показателя являются разные единицы измерения производных.
Натуральный метод (в чем заключается, формула)Натуральный метод вычисления показателя роста ПТ является наиболее точным из всех. Однако его невозможно применить на предприятиях, которые выпускают продукцию разных сортов.
При расчете объем производства выражается в килограммах, единицах, метрах, литрах и в других натуральных величинах. Вычисление происходит по формуле:
ППТ = Оп / Кр, где
ППТ –показатель производительности труда;
Оп – объем производства в кг, единицах, литрах, метрах и т.д.;
Кр – средняя численность сотрудников предприятия.
Стоимостной метод (суть, формула расчета)Стоимостной способ вычисления роста производительности труда необходим для отражения показателя, выраженного в деньгах (рублях и иностранной валюте). Он применяется для исследования трудовых затрат, оценки выработки работников разной квалификации.
Он определяется по формуле:
ППТ = ОПс / Крп, где
ОПс – стоимостное выражение объема изготовленных товаров;
Крп – число работников, изготавливающих продукцию.
Трудовой метод (в чем заключается, формула)Трудовой способ заключается в нахождении ПТ с целью сравнения реальных чисел с установленными на предприятии нормативами. Он показывает, сколько необходимо затратить труда для производства единицы товара.
ППТ = ОП1 / Кв, где
ОП1 – объем произведенных товаров за единицу затраченного времени (час, смена, сутки, неделя, месяц и т.д.).
Расчет индекса производительности труда (задачи, формула)Расчет индекса ПТ необходим для прогнозирования динамики ПТ. Он поможет предсказать, когда начнется рост или падение ПТ. Индекс рассчитывается в зависимости от выработки и трудоемкости.
Индекс рассчитывается в зависимости от выработки и трудоемкости.
В первом случае используется формула:
Ипт = ((ПВ0 – ПВ1) / ПВ1) * 100%, где
Ипт – индекс производительности труда;
ПВ0 – Показатель выработки отчетного года;
ПВ1 – показатель выработки предыдущего года.
В зависимости от трудоемкости индекс ПТ рассчитывается немного иначе:
Ипт = ((ПТ0 – ПТ1) / ПТ1) * 100%, где
Ипт – индекс производительности труда;
ПТ0 – показатель трудоемкости отчетного года;
ПТ1 – показатель трудоемкости предыдущего года.
Анализ производительности трудаАнализ ПТ позволяет понять рациональность использования ручного и автоматизированного труда. Кроме того, он помогает найти пути роста и скрытые резервы.
Исследование проводится по трем скриптам, которые выявляют обобщающие, частные и вспомогательные показатели.
Чаще всего находят выработку по годам, кварталам, месяцам, неделям, дням. Данные показатели относят к обобщающим.
Частные помогают определить количество изготовленных товаров за определенный промежуток времени. Если говорить простыми словами, то так оценивается трудоемкость.
Вспомогательные показатели необходимы для определения трудовых затрат на производство определенного вида продукта.
Анализ ПТ необходим для:
- урегулирования производственного процесса;
- увеличения объема производства;
- оптимизации сырья, материалов, оборудования.
С целью оптимизации производственного процесса предприятию предстоит решить ряд важных задач:
- покупка нового оборудования, которое поможет усовершенствовать производство, что приведет к росту объема выпускаемой продукции;
- оптимизировать управленческие процессы;
- распределить кадры, за счет чего образуется экономия труда;
- мотивировать сотрудников, для чего необходимо ввести систему поощрительных, повелительных, карательных мер;
- оптимизация оплаты труда.

Ошибка 1. На предприятии молочной промышленности, выпускающем 3 вида молока, проведен анализ ПТ с помощью натурального метода.
Решение 1. Для оценки ПТ на предприятии, выпускающем продукцию разных сортов нельзя использовать натуральный метод расчета показателя ПТ. Лучше применить трудовой или стоимостной способ. Только тогда исследование покажет более точный результат.
Ошибка 2. На предприятии, выпускающем газобетонные блоки, никогда не проводился анализ ПТ. Руководство считает исследование пустой тратой времени. За последние 2 года фирма терпит убытки, наблюдается текучка кадров.
Решение 2. Чтобы оценить деятельность предприятия, обязательно проводятся анализы. Исследование ПТ позволяет определить рациональность использовании трудовых ресурсов, поможет усовершенствовать производственный процесс, найти пути к сокращению трудовых затрат, понять причины образования текучести кадров.
Ответы на часто задаваемые вопросыРезервы роста производительности труда является достаточно сложной темой, требующей детального изучения. Понятно, что в процессе ее изучения могут возникать вопросы.
Вопрос 1. В чем отличие производительности общественного и индивидуального труда?
Ответ 1. Производительность общественного труда показывает объем изготовленной продукции всем предприятием в целом, когда производительность индивидуального труда отражает объем выпущенных товаров конкретным цехом или одним работником.
Вопрос 2. Как определить производительность труда стоимостным методом?
Ответ 2. Чтобы определить ПТ стоимостным методом, можно воспользоваться формулой:
ППТ = ОПс / Крп, где
ОПс – стоимостное выражение объема произведенной продукции;
Крп – число работников, изготавливающих продукцию.
Стоимостной способ вычисления роста производительности труда необходим для отражения показателя, выраженного в деньгах
Расчёт численности персонала
С помощью данного калькулятора вы можете расчитать целевую численность административного персонала — менеджеров и специалистов. Калькулятор позволяет объективно оценить потребности компании в персонале, спланировать оптимальную численность и расходы на персонал, повысить производительность труда.
Порядок необходимых для расчета численности операций приводится в инструкциях ниже: вы найдете примеры расчёта численности персонала, комментарии об использованных методах и формулах расчёта численности работников организации. Для демонстрации работы калькулятора мы заполнили его данными об отделе продаж условной компании, занимающейся производством строительных материалов. Вы можете заменить эти данные на информацию для собственных расчетов в оранжевых ячейках калькулятора.
Выполнение расчета численности персонала
Для расчета целевой численности персонала онлайн достаточно указать фонд рабочего времени на планируемый месяц, фактическую численность и значения драйверов численности в разделе 1 «Ввод данных для расчета». Драйвера численности – это несколько основных факторов, от которых зависит трудоёмкость работы. В нашем примере таких факторов два – количество клиентов и количество заказов в месяц. Методика определения драйверов численности будет изложена ниже.
Результаты расчета численности персонала
После ввода информации в первом разделе, вы получаете расчет целевой численности персонала в разделе 2 «Результаты расчета». Данный раздел предназначен для пользователей калькулятора — HR-менеджеров и линейных руководителей, в задачи которых входит расчёт численности персонала. Для удобства использования, калькулятор может быть внедрен на страницу внутреннего корпоративного портала вашей компании.
Какую информацию можно получить по результатам расчета численности персонала:
Целевая численность — для планирования персонала и фонда оплаты труда.
Разница с фактической численностью — для планирования мероприятий по подбору, переводу или высвобождению персонала.
Фактическая загрузка — для анализа загруженности работников и поиска возможностей ее повышения путем перераспределения функций или расширения зон ответственности.
Целевая загрузка — для анализа загруженности работников при целевой численности (нормой считается загрузка от 85% до 115%).
Изменение исходных параметров расчета численности
Следующие разделы калькулятора предназначены для специалистов по управлению персоналом. В них вы сможете задавать установленные нормы и коэффициенты, полученные в результате анализа деятельности подразделения.
Трудоемкость по должностям
В третьем разделе калькулятора «Трудоемкость по должностям» необходимо перечислить типовые должности подразделения (типовые — имеющие одинаковый функционал). Для каждой типовой должности требуется указать долю перерывов (не включая время обеда, так как оно не учитывается в норме рабочего времени) и долю ненормируемых операций. Эти параметры определяются по результатам фотографий рабочего времени. Пример разнесения операций на категории нормируемых, ненормируемых и перерывов:
Большая доля ненормируемых операций в отдельных случаях может говорить о низкой эффективности организации работы. Такая работа бывает похожа на постоянное «тушение пожаров» в неразберихе разноплановых задач. Лучшие западные практики для менеджеров — не более 30% ненормируемых операций.
В разделе 3 «Трудоемкость по должностям» также производится округление расчетной численности до целых значений (базово мы не предполагаем ввода неполных ставок). Округление производится по следующему правилу: численность округляется вверх, если после округления загрузка каждой штатной единицы не превысит 115%. То есть целевая численность менее 1,15 штатной единицы округляется до 1, а более 1,15 округляется до 2. Целевая численность менее 2,3 штатной единицы округляется до 2, а более 2,3 – до 3. И так далее. Исходя из этого принципа, любая целевая численность выше семи штатных единиц округляется в меньшую сторону.
Формула расчета численности персонала
Расчёт численности персонала в настоящем калькуляторе осуществляется по следующей формуле:
Данная общая формула может быть дополнена коэффициентом личной эффективности (оценивает индивидуальную скорость работы менеджера), долей неустранимых потерь (например, не зависящие от менеджера перерывы.) и другими важными параметрами для учета специфики подразделения.
Трудоемкость по бизнес-процессам
В разделе 4 «Трудоемкость по бизнес-процессам» разработчик калькулятора указывает бизнес-процессы подразделения, их исполнителей и трудоемкость. Важно, чтобы для каждого процесса был определен только один исполнитель (если получилось не так, процесс надо дробить). Трудоёмкость процесса определяется нормировщиком по результатам хронометражей входящих в процесс операций. В рассматриваемом нами примере карта бизнес-процессов подразделения выглядит следующим образом:
После определения бизнес-процессов и оценки их стандартной длительности остаётся сделать последний шаг в расчёте численности персонала – связать каждый бизнес-процесс с драйвером численности для определения объёма работ.
Факторы трудоемкости
Для заполнения пятого раздела калькулятора «Факторы трудоемкости» требуется определить драйвера численности. В нашем примере это количество клиентов и количество заказов. Драйверов не должно быть много, в идеале — не больше трех. Драйвера выступают первичными факторами для большинства вторичных факторов, определяющих объем работ. Например, количество новых клиентов (прирост клиентской базы) обычно коррелирует с общим количеством клиентов. Также от общего количества клиентов может статистически зависеть количество клиентов, имеющих право на скидку. Установить зависимость вторичных факторов от тех или иных драйверов можно с помощью анализа статистических данных компании.
Иногда установить драйвер для некоторых бизнес-процессов статистически не удается. В таком случае мы можем использовать константу — фиксированный объем работ, не меняющийся в течение длительного времени. В нашем случае константой установлено количество рассылок прайс-листа, так как в нашей вымышленной компании он рассылается ежедневно по рабочим дням.
Порядок заполнения пятого раздела калькулятора: 1) Определить вторичные факторы, определяющие объем работ по каждому процессу, и заполнить второй столбец; 2) Выявить драйвера численности и занести их в первый раздел калькулятора; 3) Вернуться в пятый раздел и выбрать нужные драйвера из списка, 4) Указать константы для бизнес-процессов без драйверов.
После ввода своих данных вы можете вернуться к первому разделу калькулятора и посмотреть получившийся расчёт численности персонала. Если вам требуется доработать калькулятор, скачайте Excel-файл на своей компьютер и вносите в него необходимые изменения.
Формула труда
ООО «Формула труда» оказывает профессиональные услуги по нормированию труда, планированию оптимальной численности персонала и разработке систем материального вознаграждения. Заказать наши услуги можно как в Москве, так и в других регионах России.
Как рассчитать трудоемкость в человеко месяцах
Вконтакте
Google+
Одноклассники
Здравствуйте, в этой статье мы постараемся ответить на вопрос «Как рассчитать трудоемкость в человеко месяцах». Также Вы можете бесплатно проконсультироваться у юристов онлайн прямо на сайте.
Определите трудоемкость участка по действующим нормам при учете прогрессивного использования оборудования. После этого определите пропускную способность оборудования с разделением на взаимозаменяемые группы. Для этого вначале необходимо рассчитать эффективный годовой фонд времени оборудования. Рассчитайте производственную мощность цеха, приняв в расчете производственные мощности участка.
Контрольная работа по логистике Задание 1. Материальные потоки и логистические операции: понятие, единицы измерения, классификация.
Расчет значения «человеко-час» Очень важно узнать определение этой величины. Зачем и с какой целью ее ввели, как она помогает при расчетах заработной платы и фактически отработанного времени.
Расчет для организаций с сотрудниками, работающими неполное время
Данные цифры используются при составлении отчетной документации для налоговой инспекции, Пенсионного Фонда и учреждений, осуществляющих социальную и правовую защиту населения. Помимо этого, каждое предприятие предоставляет подробные сведения о затраченных человеко-часах в «Росстат». При составлении подобной документации используется форма «П-4», которая наглядно отображает проводимые расчеты.
Если в периоде, за который подается отчет П-4, были сверхурочные часы, праздничные часы, отработанные по графику, часы работы в служебных командировках, они также включаются в расчет.
Количество человеко-часов определяют математически. Разберемся, какова формула расчета человеко часов.
Основные виды экономических ресурсов. Основы свободного предпринимательства: частная собственность, система ценообразования и конкуренция.
Расчет значения «человеко-час»
Именно поэтому каждый сотрудник бухгалтерского отдела должен знать, как считать человеко-часы. Для того чтобы получить эти экономические показатели, применяются специальные формулы, которые будут рассмотрены ниже.
Все это можно узнать ниже. Это одна из единиц расчета рабочего времени. Она показывает количество выполненной работы за один час определенного рабочего времени. Расчет этой величины позволяет оптимизировать любую работу (производства, офиса прочее).
Внедрение современных технологий, улучшение организации труда, применение в производстве качественного сырья и материалов, использование современного оборудования способствует увеличению объема производимой продукции и снижению его трудоемкости.
Учет человеко-часов и их стоимости ведется во всех организациях, где присутствуют наемные сотрудники. Это значение показывает отведенные на труд и по факту отработанные часы всего персонала.
Формула расчета трудоемкости работ
Давайте разберем, что означает данная формула. С помощью буквы «Ч» обозначаются, человеко-часы. Вместо буквы «К» подставляется количество работников в организации. «Т» — единица времени, использующаяся в расчетах. Для того чтобы упростить расчет трудозатрат, в роли единицы времени лучше всего использовать часы.
Существует и трудоемкость обслуживания производства — она включает в себя затраты на рабочую силу, связанную с обслуживанием. Для этого также просуммируйте все затраты и поделите на единицу произведенной продукции. Рассмотрите влияние отдельных факторов на рост или снижение производительности труда на вашем предприятии (качество сырья, полуфабрикатов, квалификация работников и т.д.). Сделайте необходимые выводы.
Разбираемся с вопросами по применению онлайн-кассы Порой бывает сложно самостоятельно разобраться в тонкостях «кассового» законодательства. К примеру, нужно ли выбивать чек, если за юрлицо платит физлицо и наоборот?
Привет, меня зовут Майя, просто делюсь своим опытом
К этому списку прибавляется трудоемкость обслуживания, которая отводится на вспомогательные рабочие процессы, связанные с обслуживанием производства, а также трудоемкость руководства.
Зная, насколько оперативно сотрудник способен решить конкретную задачу, можно заметно улучшить показатели эффективности и повысить производительность. Вот почему в экономической науке появилось такое понятие, как человеко-дни и человеко-часы.
При составлении производственного плана работы предприятия, организации важным моментом является расчет трудоемкости планируемых работ. Этот коэффициент рассчитывают и для анализа фактической производительности труда работников. Трудоемкость характеризует затраты труда рабочих в расчете на 1 рубль стоимости произведенной продукции.
ТРУДОЕМКОСТЬ Трудоемкость это сумма затрат живого труда в человеко-часах рабочего времени на производство единицы продукции в натуральном или стоимостном выражении как по всей номенклатуре выпуска, так и по отдельным видам работ и операций.
При составлении производственного плана работы предприятия, организации важным моментом является расчет трудоемкости планируемых работ. Этот коэффициент рассчитывают и для анализа фактической производительности труда работников. Трудоемкость характеризует затраты труда рабочих в расчете на 1 рубль стоимости произведенной продукции.
В статье рассмотрены вопросы, является ли лишение премии дисциплинарным взысканием, как выплата премии или ее лишение связаны с наличием дисциплинарного взыскания.
Как оптимизировать трудоёмкость
Если сотрудники отработали за год одинаковое количество часов, то чтобы определить по ним количество человека-часов, нужно умножить количество отработанных часов на число таких работников.
В отчетном году к работе привлекались 50 сотрудников. Из них 45 человек отработали за год по 1930 часов, а остальные 5 – по 1935 часов.
Выше мы рассмотрели, как рассчитать человеко-часы для формы П-4. Человеко-дни в этом плане менее информативны и точны, поэтому в статистических отчетах они не используются.
Человеко-час – это единица учета времени, которое занимает выполнение работы. Она соответствует одному часу работы одного человека.
Может быть как плановым — то есть рассчитываться перед началом выполнения программы, так и итоговым — оценивать, сколько человеко-часов ушло на производство заданного количества продукции по факту.
Формула расчета человеко-часов за год
Рассчитать данный коэффициент несложно — нужно количество продукции, предусмотренное планом, умножить на затраты времени (в человеко-часах) на производство одной единицы товара.
Пример 8 Два грузчика разгрузили машину с 10-тонным грузом за 6 часов. Чему равны общие и удельные трудозатраты?
Для того чтобы рассчитать полную трудоемкость, суммируйте все затраты на рабочую силу, то есть затраты на бригадиров, строителей, столяров, руководителей, специалистов и прочих работников и разделите на число выпущенных изделий.
То есть по каким именно направлениям, а также с какой интенсивностью будете проводить проверку. Для рациональной постановки задач и наилучшего обзора можете использовать графики, диаграммы или компьютерные системы.
Поэтому, если на предприятии есть работники, которые трудятся полное и неполное время, для них проводятся отдельные расчеты, с использованием табеля рабочего времени.
Суммарные человеко-часы являются результатом умножения количества работников на время, потраченное на работу. Трудоёмкость никак не может зависеть от количества работников.
Единичные нормативные трудозатраты на различные виды работ излагаются в сборниках: ЕНиР – единые нормы и расценки ВНиР – ведомственные нормы и расценки МНиР – местные нормы и расценки В сборниках на выполнение каждого вида работ приводится: полное описание состава работ по операциям, состав звена профессиональный и численный, расценки в рублях, указываются особые условия на производство работ.
После этого рассчитывается отношение величины затрат времени, выраженной в человеко-часах, к стоимости произведенных предприятием товаров. Трудоемкость управления (Тупр.).
Как посчитать человеко-часы с пояснениями и примерами
Плановая трудоемкость может быть меньше нормативной за счет планируемого снижения трудозатрат в результате организационно-технических мероприятий. Фактическая трудоемкость это сумма фактических затрат труда на фактический объем работ или выпуск продукции.
Эмоциональная составная подразумевает труд работника в коллективе (влияние рабочей единицы на трудовую атмосферу). Имиджевая составная определяет положение нового сотрудника в коллективе.
Последними может послужить отсутствие ресурсов или неисправность оборудования. Часто в подобных случаях руководство организации предупреждает работников заранее о проблемной ситуации и разрешает пропустить трудовой день.
Ее расчет производится по каждой операции, изделию либо пропорционально технологической трудоемкости изделия. Производственная трудоемкость ( ) характеризует затраты труда основных и вспомогательных рабочих на производство единицы продукции, т.е.
Зачем и с какой целью ее ввели, как она помогает при расчетах заработной платы и фактически отработанного времени. Это одна из единиц расчета рабочего времени. Эта величина более конкретная и позволяет определить равное соотношение работа–зарплата–сроки выполнения.
Разница состоит в том, что на определенную работу установлена норма времени и задействованных трудовых единиц (сюда также входит нормативная стоимость работы за 1 час определенной деятельности). Данная единица измерения позволяет определить объемную величину трудового потенциала, которая, в свою очередь, устанавливается через совокупный фонд рабочего времени.
Для начала давайте рассмотрим, что такое человеко-часы? С помощью этого термина обозначается экономическая единица, которая равняется одному часу труда N-го сотрудника. С помощью этой единицы рассчитывается временной отрезок или количество служащих, требующихся для осуществления определенной производственной задачи.
Вы можете получить бесплатную консультацию по телефону прямо сейчас. Мы работаем 24 часа в сутки, 7 дней в неделю. Ждем звонка!
Если специалист в 2018 году выполнил полную норму отведенного времени по рабочему табелю 40-часовой трудовой недели, число человеко-часов будет равняться 1970.
Часто бывает так, что сотрудники предприятия работают неполное время, например, матери, которые используют скользящий график или те, кто принят на работу на четырехчасовой рабочий день.
Трудоемкость управления ( ) оценивается затратами труда руководителей, специалистов, административного персонала, охраны и т.п.
Вконтакте
Google+
Одноклассники
Похожие записи:
Как найти временную сложность алгоритма
Грубо говоря, временная сложность — это способ суммировать, как количество операций или время выполнения алгоритма растет с увеличением размера ввода.
Как и большинство вещей в жизни, коктейльная вечеринка может помочь нам понять.
О (н.)
Когда вы приходите на вечеринку, вы должны пожать всем руки (проделать операцию с каждым предметом). По мере увеличения числа участников N время / работа, которые потребуются вам, чтобы пожать всем руку, возрастают до O (N) .
Почему O (N) , а не cN ?
Время, необходимое для рукопожатия, варьируется. Вы можете усреднить это и зафиксировать в константе c . Но основная операция здесь — рукопожатие со всеми — всегда будет пропорциональна O (N) , независимо от того, что такое c . Обсуждая вопрос о том, стоит ли нам пойти на коктейльную вечеринку, мы часто больше заинтересованы в том, что нам придется встретиться со всеми, чем в мельчайших деталях того, как выглядят эти встречи.3)
Вы должны встречаться со всеми, и во время каждой встречи вы должны говорить обо всех, кто находится в комнате.
О (1)
Хост хочет что-то объявить. Они колют рюмку и громко разговаривают. Их слышат все. Оказывается, не имеет значения, сколько посетителей, эта операция всегда занимает одинаковое количество времени.
O (лог. N)
Ведущий разложил всех за столом в алфавитном порядке.Где Дэн? Вы считаете, что он должен быть где-то между Адамом и Мэнди (уж точно не между Мэнди и Заком!). Учитывая это, он между Джорджем и Мэнди? Нет. Он должен быть между Адамом и Фредом и между Синди и Фредом. И так далее … мы можем эффективно определить местонахождение Дэна, посмотрев на половину набора, а затем на половину этого набора. В конечном итоге мы смотрим на O (log_2 N) человек.
O (N лог. N)
Вы можете найти, где сесть за стол, используя алгоритм, описанный выше.Если большое количество людей подходило к столу, по одному, и все это делали, это заняло бы O (N log N) времени. Оказывается, это время, необходимое для сортировки любой коллекции элементов, когда их нужно сравнивать.
Лучший / худший случай
Вы прибыли на вечеринку и вам нужно найти Иниго — сколько времени это займет? Это зависит от того, когда вы приедете. Если все слоняются вокруг, вы попали в худший вариант: это займет O (N) времени. Однако, если все сядут за стол, потребуется всего O (log N) времени.Или, может быть, вы можете использовать силу крика хозяина, и это займет всего O (1) времени.
Предполагая, что хост недоступен, мы можем сказать, что алгоритм поиска Inigo имеет нижнюю границу O (log N) и верхнюю границу O (N) , в зависимости от состояния стороны, когда ты приезжаешь.
Космос и связь
Те же идеи можно применить для понимания того, как алгоритмы используют пространство или связь.
Кнут написал прекрасную статью о первом, озаглавленную «Сложность песен».
Теорема 2: Существуют сколь угодно длинные песни сложности O (1).
ДОКАЗАТЕЛЬСТВО: (из-за Кейси и группы Sunshine Band). Рассмотрим песни Sk, определенные формулой (15), но с
V_k = 'Вот так,' U 'Мне это нравится,' U
U = 'ага' 'ага'
для всех k.
Как рассчитать временную сложность O (n) алгоритма?
Определим N как один из возможных входов данных.Алгоритм может иметь разные значения Big O в зависимости от того, на какой ввод вы ссылаетесь, но обычно есть только один большой ввод, который вас интересует. Без рассматриваемого алгоритма можно только догадываться. Однако есть несколько рекомендаций, которые помогут вам определить, что это такое.
Общее правило:
O (1) — скорость работы программы практически не меняется независимо от размера данных. Для этого в программе вообще не должно быть циклов, работающих с рассматриваемыми данными.
O (log N) — программа немного замедляется при резком увеличении N на логарифмической кривой. Чтобы получить это, циклы должны проходить только часть данных. (например, бинарный поиск).
O (N) — скорость программы прямо пропорциональна размеру вводимых данных. Если вы выполните операцию с каждой единицей данных, вы получите это. У вас не должно быть никаких вложенных циклов (которые воздействуют на данные).
O (N log N) — скорость программы значительно снижается из-за большего ввода.2).
Также помните, что у вас могут быть петли под капюшоном, так что вам тоже стоит подумать о них. Например, если вы сделали что-то вроде Arrays.sort (X) в Java, это будет операция O (N logN). Так что, если по какой-то причине у вас есть это внутри цикла, ваша программа будет намного медленнее, чем вы думаете.
Надеюсь, что это ответ на ваш вопрос.
Считайте свои шаги · YourBasic
yourbasic.org
Сложность времени оценивает время выполнения алгоритма.Он рассчитывается путем подсчета элементарных операций.
Пример (итерационный алгоритм)
Каково время работы следующего алгоритма?
// Вычислить максимальный элемент в массиве a.
Алгоритм max (a):
max ← a [0]
для i = 1 от до len (a) -1
, если a [i]> max
max ← a [i]
возврат макс.
Ответ зависит от таких факторов, как ввод, язык программирования и время выполнения, навыки программирования, компилятор, операционная система и оборудование.
Мы часто хотим рассуждать о времени выполнения таким образом, чтобы только на алгоритме и его входе . Этого можно добиться, выбрав элементарную операцию , который алгоритм выполняет неоднократно, и определить временная сложность T ( n ) как количество таких операций алгоритм выполняет заданный массив длиной n .
Для алгоритма выше мы можем выбрать сравнение a [i]> max как элементарная операция.
- Это хорошо отражает время работы алгоритма, поскольку сравнения преобладают над всеми другими операциями в этом конкретном алгоритме.
- Кроме того, время выполнения сравнения постоянно:
это не зависит от размера
a.
Временная сложность, измеряемая количеством сравнений, тогда становится T ( n ) = n — 1.
Как правило, элементарная операция должна иметь два свойства:
- Других операций, выполняемых чаще, быть не может. по мере роста размера ввода.
- Время выполнения элементарной операции должно быть постоянным: он не должен увеличиваться по мере увеличения размера ввода. Это называется себестоимостью единицы.
Временная сложность наихудшего случая
Рассмотрим этот алгоритм.
// Сообщаем, содержит ли массив a x.
Алгоритм содержит (a, x):
для i = 0 от до len (a) -1
, если x == a [i]
возврат истина
возврат ложь
В этом случае сравнение x == a [i] может использоваться как элементарная операция.Однако для этого алгоритма количество сравнений зависит не только от количества элементов, n ,
в массиве, но также от значения x и значений в a :
- Если
xне найдено вa, алгоритм выполняет сравнения n , - , но если
xравноa [0], есть только одно сравнение.
Из-за этого мы часто выбираем для изучения наихудший случай временной сложности:
- Пусть T 1 ( n ), T 2 ( n ),… время выполнения для всех возможных вводов типоразмера n .
- Тогда временная сложность W для наихудшего случая ( n ) определяется как W ( n ) = max (T 1 ( n ), T 2 ( n ),…).
Наихудшая временная сложность для содержит алгоритм , таким образом становится
W ( n ) = n .
Временная сложность наихудшего случая дает верхнюю границу требований ко времени и часто легко вычисляется. Недостаток в том, что он часто бывает излишне пессимистичным.
См. Временная сложность операций с массивами / списками для подробного ознакомления с производительностью основных операций с массивами.
Средняя временная сложность
Средний случай Временная сложность — менее распространенная мера:
- Пусть T 1 ( n ), T 2 ( n ),… время выполнения
для всех возможных входов размера n ,
и пусть P 1 ( n ), P 2 ( n ),… быть вероятностями этих входов. - Средняя временная сложность определяется как P 1 ( n ) T 1 ( n ) + P 2 ( n ) T 2 ( n ) +…
Среднее время часто труднее вычислить, и это также требует знания того, как распределяется ввод.
Квадратичная временная сложность
Наконец, мы рассмотрим алгоритм с низкой временной сложностью.
// Обратный порядок элементов в массиве a.
Алгоритм обратный (а):
для i = 1 от до len (a) -1
x ← a [i]
для j = i до 1
a [j] ← a [j-1]
а [0] ← х
Выбираем присвоение a [j] ← a [j-1] как элементарную операцию.
Обновление элемента в массиве — это операция с постоянным временем,
и назначение доминирует над стоимостью алгоритма.
Количество элементарных операций полностью определяется размером ввода n . Фактически, внешний цикл for выполняется n — 1 раз. Таким образом, временная сложность становится
.Вт ( n ) = 1 + 2 +… + ( n — 1) = n ( n — 1) / 2 = n 2 /2 — n /2.
Квадратичный член доминирует для больших n , и поэтому мы говорим, что этот алгоритм имеет квадратичную временную сложность .Это означает, что алгоритм плохо масштабируется и может использоваться только для небольшого ввода : чтобы перевернуть элементы массива из 10 000 элементов, алгоритм выполнит около 50 000 000 заданий.
В этом случае легко найти алгоритм с линейной временной сложностью .
Алгоритм обратный (а):
для i = 0 от до n / 2
поменять местами a [i] и a [n-i-1]
Это на огромное улучшение по сравнению с предыдущим алгоритмом: массив из 10000 элементов теперь можно перевернуть всего с 5000 свопами, т.е.е. 10000 заданий. Это примерно в 5000 раз больше скорости, и улучшение продолжает расти по мере увеличения ввода.
Обычно используется нотация Big O когда говорят о временной сложности. Тогда мы могли бы сказать, что временная сложность первого алгоритма Θ ( n 2 ), и что улучшенный алгоритм имеет временную сложность ( n ).
Дополнительная литература
Обозначение Big O
Временная сложность операций с массивами / списками [Java, Python]
Временная сложность рекурсивных функций [Основная теорема]
Поделиться:
Анализ алгоритмов | Набор 4 (Анализ петель)
Мы обсуждали асимптотический анализ, наихудшие, средние и наилучшие случаи и асимптотические обозначения в предыдущих постах.В этом посте обсуждается анализ итерационных программ на простых примерах.
1) O (1): Временная сложность функции (или набора операторов) рассматривается как O (1), если она не содержит цикла, рекурсии и вызова любой другой функции с непостоянным временем.
// набор нерекурсивных и нециклических операторов
Например, функция swap () имеет временную сложность O (1).
Цикл или рекурсия, которые выполняются постоянное количество раз, также рассматриваются как O (1).Например, следующий цикл — O (1).
// Здесь c - постоянная
for (int i = 1; i <= c; i ++) {
// некоторые выражения O (1)
} 2) O (n): Время Сложность цикла рассматривается как O (n), если переменные цикла увеличиваются / уменьшаются на постоянную величину. Например, следующие функции имеют временную сложность O (n).
// Здесь c - положительная целочисленная константа
for (int i = 1; i <= n; i + = c) {
// некоторые выражения O (1)
}
for (int i = n; i> 0; i - = c) {
// некоторые выражения O (1)
} 3) O (n c ) : Временная сложность вложенных циклов равна количеству выполнений самого внутреннего оператора.Например, следующие примеры циклов имеют временную сложность O (n 2 )
for (int i = 1; i <= n; i + = c) {
for (int j = 1; j <= n; j + = c) {
// некоторые выражения O (1)
}
}
for (int i = n; i> 0; i - = c) {
for (int j = i + 1; j <= n; j + = c) {
// некоторые выражения O (1)
} Например, сортировка выбора и сортировка вставкой имеют временную сложность O (n 2 ).
4) O (Logn) Время Сложность цикла рассматривается как O (Logn), если переменные цикла делятся / умножаются на постоянную величину.
для (int i = 1; i <= n; i * = c) {
// некоторые выражения O (1)
}
for (int i = n; i> 0; i / = c) {
// некоторые выражения O (1)
} Например, двоичный поиск (см. Итеративную реализацию) имеет временную сложность O (Logn). Давайте посмотрим математически, как это O (Log n). Ряд, который мы получаем в первом цикле, - это 1, c, c 2 , c 3 ,… c k .Если мы положим k равным Log c n, мы получим c Log c n , который равен n.
5) O (LogLogn) Время Сложность цикла рассматривается как O (LogLogn), если переменные цикла уменьшаются / увеличиваются экспоненциально на постоянную величину.
// Здесь c - константа больше 1
for (int i = 2; i <= n; i = pow (i, c)) {
// некоторые выражения O (1)
}
// Здесь fun - это sqrt или cuberoot или любой другой постоянный корень
for (int i = n; i> 1; i = fun (i)) {
// некоторые выражения O (1)
} См. Здесь для математических подробностей.
Как совместить временные сложности последовательных циклов?
Когда есть последовательные циклы, мы вычисляем временную сложность как сумму временных сложностей отдельных циклов.
для (int i = 1; i <= m; i + = c) {
// некоторые выражения O (1)
}
for (int i = 1; i <= n; i + = c) {
// некоторые выражения O (1)
}
Временная сложность приведенного выше кода составляет O (m) + O (n), что составляет O (m + n)
Если m == n, временная сложность становится O (2n), что составляет O (n). Как рассчитать временную сложность, когда внутри циклов много операторов if, else?
Как обсуждалось здесь, временная сложность наихудшего случая является наиболее полезной среди наилучших, средних и наихудших. Поэтому нам нужно рассматривать худший случай. Мы оцениваем ситуацию, когда значения в условиях if-else вызывают выполнение максимального числа операторов.
Например, рассмотрим функцию линейного поиска, в которой мы рассматриваем случай, когда элемент присутствует в конце или отсутствует вовсе.
Когда код слишком сложен для рассмотрения всех случаев if-else, мы можем получить верхнюю границу, игнорируя if else и другие сложные управляющие операторы.
Как вычислить временную сложность рекурсивных функций?
Временная сложность рекурсивной функции может быть записана как математическое рекуррентное соотношение. Чтобы вычислить временную сложность, мы должны знать, как решать повторения. Вскоре мы обсудим методы решения проблем с повторениями как отдельный пост.
Викторина по анализу алгоритмов
Далее - Анализ алгоритма | Набор 4 (Решение повторений)
Пожалуйста, напишите комментарий, если вы обнаружите что-то неправильное, или если вы хотите поделиться дополнительной информацией по теме, обсужденной выше.
Вниманию читателя! Не прекращайте учиться сейчас. Ознакомьтесь со всеми важными концепциями DSA с помощью курса DSA Self Paced Course по доступной для студентов цене и подготовьтесь к работе в отрасли.
Сложность алгоритмов
Сложность алгоритмов- Весь смысл большого O / Ω / был в том, чтобы иметь возможность сказать что-то полезное об алгоритмах.
- Итак, вернемся к некоторым алгоритмам и посмотрим, научились ли мы чему-нибудь.
- Рассмотрим эту простую процедуру суммирования списка (мы предполагаем, что числа):
сумма процедуры (список) всего = 0 для i от 0 до длины (список) -1 total + = list [i] вернуть итог- Во-первых: правильный ли алгоритм? Решает ли это указанную проблему?
- Секунда: это быстро?
- Чтобы оценить время работы алгоритма, мы просто спросим, сколько «шагов» он занимает.
- В этом случае мы можем подсчитать, сколько раз он запускал строку
+ =. - Для списка с \ (n \) элементами требуется \ (n \) шагов.
- В этом случае мы можем подсчитать, сколько раз он запускал строку
- Или правильно ли считать строку
+ =?- При реализации цикла
длякаждая итерация требует добавления (для индекса цикла) и сравнения (для проверки условия выхода). Мы должны их посчитать. - Кроме того, инициализация переменной и
возвращаютшагов. - Итак, \ (3n + 2 \) шагов.
- При реализации цикла
- Но не все эти шаги одинаковы.
- Сколько времени занимает инструкция x86 ADD по сравнению с инструкцией CMP или RET?
- Будет ли компилятор хранить
iи, всегов регистрах, или один / оба будут в ОЗУ? (Разница в ~ 10 раз.) - Как эти инструкции взаимодействуют в конвейере? Что может быть отправлено через параллельные конвейеры в процессоре и выполнено одновременно?
- Ответ на них прост: я не знаю, и вы тоже.
- Это одна из причин, по которой мы спрашиваем об алгоритмах, а не о программах.
- Но и \ (n \), и \ (3n + 2 \) - вполне разумные предложения для ответа.
- Выбор между ними требует большего знания фактических деталей реализации, чем у нас.
- Хорошо, что у нас есть обозначение роста функции.
- Помните: это просто для элементов \ (n = 5 \). Тогда и хороший, и плохой алгоритм будет быстрым.
- Мы хотим знать, как алгоритм ведет себя для больших \ (n \).
- Наконец, наш ответ: процедура
sumимеет время выполнения \ (\ Theta (n) \).- Мы скажем, что этот алгоритм имеет временную сложность \ (\ Theta (n) \) или «работает за линейное время».
- И \ (n \), и \ (3n + 2 \) равны \ (\ Theta (n) \), как и любая другая «точная» формула, которую мы могли бы придумать.
- Простой ответ (посчитайте строку
+ =) был столь же правильным, как и очень осторожный. - Обозначение большого скрывает все детали, которые мы в любом случае не можем понять.
- Другой пример: распечатайте сумму каждых двух чисел в списке.
- То есть, учитывая список [1,2,3,4,5], мы хотим найти 1 + 2, 1 + 3, 1 + 4, 1 + 5, 2 + 3, 2 + 4,….
- Псевдокод:
процедура sum_pairs (список) для i от 0 до длины (список) -2 для j от i + 1 до длины (список) -1 распечатать список [i] + список [j] - Для списка с элементами \ (n \) цикл
for jповторяется \ (n-1 \) раз, когда он вызывается сi == 0, затем \ (n-2 \) раз, затем \ (n-3 \) раз,… - Итак, общее количество прогонов шага
printравно \ [\ begin {align *} (n-1) + (n-2) + \ cdots + 2 + 1 & = \ sum_ {k = 1} ^ {n-1} k \\ & = \ frac {n (n-1)} {2 } \\ & = \ frac {n ^ 2} {2} - \ frac {n} {2} \ ,.2) \) время работы »или« имеет квадратичное время работы ».
- Урок: при подсчете времени бега можно быть немного небрежным.
- Нам нужно беспокоиться только о самом внутреннем цикле (ах), а не о количестве шагов в нем или работе на внешних уровнях.
- … потому что они все равно исчезнут как постоянные множители и члены более низкого порядка, когда они все равно войдут в большой O / Ω /.
- Рассмотрим линейный поиск : мы хотим найти элемент в списке и вернуть его (первую) позицию или -1, если его там нет.
процедура linear_search (список, значение) для i от 0 до длины (список) -1 если список [i] == значение вернуть я возврат -1 - Ответ: это зависит от обстоятельств.
- Если объект, который мы ищем, находится на первой позиции, он требует \ (\ Theta (1) \) шагов.
- Если он в конце или не там, требуется \ (\ Theta (n) \) шагов.
- Обычно проще всего сосчитать наихудший случай : какие максимальные шагов требуются для любого ввода размера \ (n \)?
- В худшем случае мы доходим до конца списка, но не находим его и возвращаем -1.
- Единственная строка, которую имеет смысл считать здесь, - это строка
if. Он находится в самом внутреннем цикле и выполняется для каждой итерации. - Мы также можем подсчитать количество сравнений, сделанных :
==и неявное сравнение в цикледля. - Это либо \ (n \), либо \ (2n + 1 \) шагов, поэтому сложность \ (\ Theta (n) \).
- Другой полезный вариант - это средний случай : какие средних шагов требуются для всех входов размера \ (n \)?
- Гораздо сложнее вычислить, поскольку вам нужно учитывать все возможные входные данные для алгоритма.
- Даже если мы предположим, что элемент найден, возможное количество сравнений:
Найдено в позиции Сравнения 1 2 2 4 & vellip; & веллип; \ (п \) \ (2н \) - В среднем количество сравнений составляет:
\ [\ frac {2 + 4 + \ cdots + 2n} {n} = n + 1 \,. n \)
\ (10 \) 3.n) \) - это катастрофа: почти так же плохо, как отсутствие алгоритма, если у вас есть двузначные входные размеры. Это алгоритмов экспоненциальной сложности для \ (k \ gt 1 \). - См. Также: Числа, которые должен знать каждый
- Задача, имеющая алгоритм с полиномиальным временем, называется решаемой .
- Нет алгоритма полиномиального времени: трудноразрешимый .
- Существует большая категория задач, для которых ни у кого нет алгоритма полиномиального времени, но также не может доказать, что его не существует: NP-полных задач .2 \) инструкция по решению проблемы.
- Когда у вас есть правильный большой О, пора беспокоиться о константах.
- Вот на что способно умное программирование.
- Когда мы говорим об алгоритмах (а не о программировании), константы обычно не имеют особого значения .
- Алгоритм с большой ведущей константой - редкость.
- Значит, выбор между алгоритмами невозможен.
- Обычно это выбор между \ (4n \ log n \) или \ (5n \ log n \): вам, вероятно, придется реализовать, скомпилировать и профилировать, чтобы решить наверняка.2) \) худший случай.
- Но на практике быстрая сортировка обычно быстрее.
- … кроме случаев, когда это не так.
- Несколько последних языков / библиотек реализовали сильно оптимизированную сортировку слиянием (например, Python, Perl, Java ≥JDK1.3, Haskell, некоторые реализации STL) вместо быстрой сортировки (C, Ruby, некоторые другие реализации STL).
- До сих пор мы говорили только о времени / скорости работы.
- Также имеет смысл поговорить о сложности других вещей.{3}) \) время.
- Алгоритм, использующий \ (O (1) \) дополнительное пространство (в дополнение к пространству, необходимому для хранения ввода), называется на месте .
- например сортировка по выбору выполняется на месте, но сортировка слиянием (\ (\ Theta (n) \) дополнительное пространство) и быстрая сортировка (\ (\ Theta (\ log n) \) дополнительное пространство, средний регистр) - нет.
Вернуться на главную страницу заметок к курсу. Авторские права © 2013, Грег Бейкер.
Учебных пособий и примечаний по сложности времени и пространства | Базовое программирование
Иногда есть несколько способов решить проблему.Нам нужно научиться сравнивать производительность разных алгоритмов и выбирать лучший для решения конкретной задачи. При анализе алгоритма мы в основном учитываем временную сложность и пространственную сложность. Сложность алгоритма по времени определяет количество времени, затрачиваемое алгоритмом на выполнение, в зависимости от длины входных данных. Точно так же пространственная сложность алгоритма количественно определяет объем пространства или памяти, занимаемой алгоритмом для работы, в зависимости от длины входных данных.
Сложность времени и пространства зависит от множества вещей, таких как оборудование, операционная система, процессоры и т. Д.Однако мы не учитываем ни один из этих факторов при анализе алгоритма. Мы будем рассматривать только время выполнения алгоритма.
Начнем с простого примера. Предположим, вам дан массив $$ A $$ и целое число $$ x $$ и вам нужно выяснить, существует ли $$ x $$ в массиве $$ A $$.
Простое решение этой проблемы - пройти весь массив $$ A $$ и проверить, равен ли любой элемент $$ x $$.
для i: от 1 до длины A если A [i] равно x вернуть ИСТИНА вернуть ЛОЖЬКаждая операция на компьютере занимает приблизительно постоянное время.Пусть каждая операция занимает $$ c $$ времени. Количество выполняемых строк кода фактически зависит от значения $$ x $$. При анализе алгоритма в основном мы будем рассматривать наихудший сценарий, т.е. когда $$ x $$ отсутствует в массиве $$ A $$. В худшем случае условие if будет выполняться $$ N $$ раз, где $$ N $$ - длина массива $$ A $$. Таким образом, в худшем случае общее время выполнения будет $$ (N * c + c) $$. $$ N * c $$ для условия if и $$ c $$ для оператора return (игнорируя некоторые операции, такие как присвоение $$ i $$).
Как мы видим, общее время зависит от длины массива $$ A $$. Если длина массива увеличится, время выполнения также увеличится.
Порядок роста - это то, как время выполнения зависит от длины ввода. В приведенном выше примере мы ясно видим, что время выполнения линейно зависит от длины массива. Порядок роста поможет нам легко вычислить время работы. Мы проигнорируем члены более низкого порядка, поскольку члены более низкого порядка относительно несущественны для больших входных данных.Мы используем разные обозначения для описания предельного поведения функции.
$$ O $$ - обозначение:
Для обозначения асимптотической верхней границы используется обозначение $$ O $$. Для данной функции $$ g (n) $$ мы обозначаем через $$ O (g (n)) $$ (произносится как «big-oh of g of n») набор функций:
$$ O (g (n)) = $$ {$$ f (n) $$: существуют положительные константы $$ c $$ и $$ n_0 $$ такие, что $$ 0 \ le f (n) \ le c * g (n) $$ для всех $$ n \ ge n_0 $$}$$ \ Omega $$ - обозначение:
Для обозначения асимптотической нижней границы используется обозначение $$ \ Omega $$.Для данной функции $$ g (n) $$ мы обозначаем через $$ \ Omega (g (n)) $$ (произносится как «большая омега из g из n») набор функций:
$$ \ Omega (g (n)) = $$ {$$ f (n) $$: существуют положительные константы $$ c $$ и $$ n_0 $$ такие, что $$ 0 \ le c * g (n) \ le f ( n) $$ для всех $$ n \ ge n_0 $$}$$ \ Theta $$ - обозначение:
Для обозначения асимптотической точной границы мы используем обозначение $$ \ Theta $$. Для данной функции $$ g (n) $$ мы обозначаем через $$ \ Theta (g (n)) $$ (произносится как «большая тета от g из n») набор функций:
$$ \ Theta (g (n)) = $$ {$$ f (n) $$: существуют положительные константы $$ c_1, \; c_2 $$ и $$ n_0 $$ такие, что $$ 0 \ le c_1 * g (n) \ le f (n) \ le c_2 * g (n) $$ для всех $$ n \ gt n_0 $$}Обозначения временной сложности
При анализе алгоритма мы в основном рассматриваем нотацию $$ O $$, потому что она дает нам верхний предел времени выполнения i.2) $$
Давайте рассмотрим пример:
1.
int count = 0; для (int i = 0; iДавайте посмотрим, сколько раз будет выполнено count ++ .
Когда $$ i = 0 $$, он будет выполняться $$ 0 $$ раз.
Когда $$ i = 1 $$, он будет выполняться $$ 1 $$ раз.
Когда $$ i = 2 $$, он будет выполняться $$ 2 $$ раз и так далее.Общее количество запусков count ++ составляет $$ 0 + 1 + 2 +.2) $$.
2.
Это непростой случай. На первый взгляд кажется, что сложность составляет $$ O (N * logN) $$. $$ N $$ для цикла $$ j $$ и $$ logN $$ для цикла $$ i $$. Но это неправильно. Посмотрим почему.int count = 0; для (int i = N; i> 0; i / = 2) для (int j = 0; jПодумайте, сколько раз будет выполнено count ++ .
Когда $$ i = N $$, он будет выполняться $$ N $$ раз.
Когда $$ i = N / 2 $$, он будет выполняться $$ N / 2 $$ раз.
Когда $$ i = N / 4 $$, он будет запускать $$ N / 4 $$ раз и так далее.Общее количество запусков count ++ : $$ N + N / 2 + N / 4 + ... + 1 = 2 * N $$. Таким образом, временная сложность будет $$ O (N) $$.
Приведенная ниже таблица поможет вам понять рост нескольких общих временных сложностей и, таким образом, поможет вам оценить, достаточно ли быстр ваш алгоритм, чтобы получить оценку «Принято» (при условии, что алгоритм правильный).
Длина входа (N) Худший принятый алгоритм $$ \ le [10.2) $$ $$ \ le 1M $$ $$ O (N * logN) $$ $$ \ le 100M $$ $$ O (N), O (logN), O (1) $$ Перейти к следующему руководству
Прислал: Акаш Шарма
Big O: Как вычислить временную и пространственную сложность
Что такое Big O?
НотацияBig O используется для количественной оценки того, насколько быстро будет расти время выполнения или использование памяти при запуске алгоритма в наихудшем сценарии относительно размера входных данных ( n ).Его также иногда называют асимптотической верхней оценкой.
Мы можем использовать нотацию Big O для описания двух вещей:
- Сложность времени
Насколько быстро растет продолжительность алгоритма относительно входа - Сложность пространства
Сколько места требуется алгоритму по мере его роста
В этом руководстве вы узнаете, как использовать нотацию Big O , с понятными примерами кода с комментариями.
Зачем нужна большая буква O?
Для любой проблемы может быть множество решений.Но если вы измеряете время выполнения в секундах, вы подвержены колебаниям, вызванным физическими факторами. Сюда входит объем памяти на машине, используемой для запуска решения, скорость ЦП и других программ, одновременно работающих в системе.
Big O используется для сравнения эффективности решения без учета физических факторов.
Каждый алгоритм имеет свои пространственные и временные сложности. Во многих ситуациях лучшим решением будет баланс двух.
Например, если нам нужно быстрое решение, и нас не слишком беспокоят требования к пространству, приемлемым компромиссом может быть алгоритм с меньшей временной сложностью и более высокой сложностью пространства.например Сортировка слиянием.
Итак, как вы вычисляете Big O для данного алгоритма?
Как рассчитать Big O
Чтобы вычислить Big O, сначала нужно учесть, сколько операций выполняется.
Простое руководство из 5 шагов:
- Разделите алгоритм на операции
- Вычислить "О" каждой операции
- Добавьте большой O из каждой операции
- Убрать константы
- Найдите член высшего порядка
В примерах ниже подробно описан каждый шаг, но стоит упомянуть, почему мы исключили константы.
Наше определение Big O включало фразу «относительно размера входных данных ( n )». Это означает, что по мере того, как n получает произвольно большие операции фиксированного размера, такие как добавление 100 или деление на 2, имеют все менее значимое влияние на время, необходимое для выполнения алгоритма.
По той же причине мы ищем наиболее значимый термин. Big O измеряет наихудший случай, что означает, что мы всегда должны использовать самую медленную временную сложность для любой операции в алгоритме.Поскольку n становится произвольно большим, менее значимые термины не будут иметь такого же влияния на время выполнения, как наиболее значимые термины.
Пример 1: сложение двух чисел
def add_nums (числа): total = nums [0] + nums [1] # O (1) - Константа общая сумма возврата # O (1) - Постоянная add_nums ([1, 2, 3])
В примере 1 мы добавляем два числа из заданного списка, выполняя поиск по индексу.
Для
total = nums [0] + nums [1]мы выполняем три операции, каждая из которых имеет постоянную временную сложность O (1):- Операция 1:
nums [0] - это поиск.О (1) - Operation 2:
nums [1] - это поиск. n)
Сложность времени
Постоянное время: O (1)
Свойства алгоритма с постоянной временной сложностью :
- Время выполнения алгоритма не зависит от размера входных данных
- Сложность времени всегда одинакова, независимо от ввода
Некоторые операции с временной сложностью O (1):
- получить элемент (поиск по индексу / ключу)
- комплект (назначение)
- арифметическая операция (e.грамм. 1 + 1, 2 - 1 и т. Д.)
- сравнительный тест (например, x == 1)
Любой метод, который выполняет фиксированное количество основных операций при каждом вызове, требует постоянного времени.
Пример 1: Получить значение индексаdef get_first (данные): вернуть данные [0] данные = [1, 2, 9, 8, 3] печать (get_first (данные))При получении значения элемента по определенному индексу сложность времени составляет O (1). В приведенном выше примере, содержит ли наш список 5 элементов или 500, сложность получения значения по индексу 0 остается равной O (1).
Причина этого в том, что операции, необходимые для доступа к элементу в памяти, остаются постоянными, независимо от того, сколько элементов находится в массиве.
Учитывая начальный адрес в памяти массива, вы можете просто умножить размер типа данных в байтах на индекс элемента, который вы ищете.
Пример: Начальный адрес массива - 10. Поиск 5-го элемента в массиве целых чисел. Целочисленный тип данных - 4 байта. Итак, адрес искомого товара:
.(10 + (5 * 4))Логарифмическое время: O (log n)
Свойства алгоритма с логарифмической временной сложностью :
- Уменьшает размер входных данных на каждом шаге
- Не нужно смотреть на все значения
- Следующее действие будет выполнено только с одним из нескольких возможных элементов
Примеры операций: Двоичный поиск, операции с деревьями двоичного поиска
Считается, что алгоритмы с подходом «разделяй и властвуй» имеют логарифмическую временную сложность, например бинарный поиск.
Пример 1: Распечатать каждое третье значение в диапазоне
для индекса в диапазоне (0, len (данные), 3): print (данные [индекс])Пример 2: Найти значение с помощью двоичного поиска
def binarySearch (sortedList, цель): left = 0 right = len (sortedList) - 1 пока (слева
Линейное время: O (n)
Свойства алгоритма с линейной временной сложностью :
- Количество выполняемых операций линейно масштабируется размером n
- e.грамм. Выполнение операции печати 100 раз по одному на элемент в списке, содержащем 100 элементов
Примеры операций: копирование, вставка в массив, удаление из массива, итерация
Алгоритмы: Линейный поиск
Алгоритм с линейной временной сложностью считается оптимальным решением, когда необходимо проверить все значения.
Пример 1: Распечатать каждое значение в диапазоне
данных = [1, 7, 3, 19, 2, 100] для индекса в диапазоне (len (данные)): print (данные [индекс])В приведенном выше примере сама операция печати - O (1), но количество итераций, которые мы выполняем в цикле
Пример 2: Печатать каждое значение в n дважды, как две отдельные операциидля, прямо пропорционально размеру входных данных.Поскольку мы всегда берем член более высокого порядка, временная сложность Big O равна O (n).def print_twice (lst): # O (n) - O (2n), но мы опускаем константу для val в lst: # O (n) распечатать val для val в lst: # O (n) распечатать val
В примере 2 мы объединяем две временные сложности, чтобы получить
O (n) + O (n) = O (2n). Теперь мы опускаем константу (2), чтобы получить O (n).Пример 3: Найти элемент в отсортированном списке
def linearSearch (sortedList, цель): для i в диапазоне (len (sortedList)): if (sortedList [i] == target): вернуть я # Если цель отсутствует в списке, вернуть -1 возврат -1 linearSearch ([1,3,9,22], 22) # return 3В примере 3 мы выполняем линейный поиск в отсортированном массиве.Более быстрый подход, поскольку массив отсортирован, заключался бы в использовании двоичного поиска, который имеет логарифмическую временную сложность O (log n).
Квазилинейное время: O (n log n)
Свойства алгоритма с логарифмической линейной (также известной как квазилинейной ) временной сложностью:
- Каждая операция во входных данных имеет логарифмическую временную сложность
- например для каждого значения в data1 (O (n)) используйте двоичный поиск (O (log n)) для поиска того же значения в data2
Примеры операций: Сортировать список
Алгоритмы с временной сложностью O (n log n):
- Слияние
- Heapsort
- Cubesort
Пример 1:
для значения в data1: результат.п)Свойства алгоритма с экспоненциальной временной сложностью:
- Рост удваивается с каждым добавлением к набору исходных данных
- например Проблема "Ханойских башен"
Алгоритмы: Рекурсивный Фибоначчи
Пример 1: Рекурсивное вычисление чисел Фибоначчи
def fibonacci (число): если (число
Факториальное время: O (n!)
Свойства алгоритма с факториалом Временная сложность:
- Факториальное увеличение в зависимости от размера входных данных
- Быстро разрастается даже при небольших размерах материала
Пример 1: алгоритм кучи
def heap_permutation (данные, n): если n == 1: печать (данные) возвращаться для i в диапазоне (n): heap_permutation (данные, n - 1) если n% 2 == 0: данные [i], данные [n-1] = данные [n-1], данные [i] еще: данные [0], данные [n-1] = данные [n-1], данные [0] данные = [1, 2, 3] heap_permutation (данные, len (данные))Космическая сложность
В некоторых ситуациях мы хотим оптимизировать пространство, а не время, или найти баланс между ними.Для этого нам нужно рассчитать сложность пространства.
Сложность пространства измеряется с использованием тех же обозначений, что и временная сложность, но мы учитываем необходимое общее выделение памяти относительно размера ввода.
Пример 1: O (n) пространственная сложность
def create_list (n): new_list = [] для числа в диапазоне (n): new_list.append ('новый') вернуть новый_лист create_list (5) # ['новый', 'новый', 'новый', 'новый', 'новый']Приведенный выше код имеет пространственную сложность O (n), поскольку объем необходимого пространства увеличивается с размером n (линейный).
Пример 2: сложность пространства O (1)
def hello_world (n): for x in range (len (n)): # Сложность времени - O (n) print ('Hello World!') # Сложность пространства - O (1)В примере 2 количество повторений цикла прямо пропорционально размеру входных данных. Следовательно, у нас есть линейная временная сложность O (n).
Операция
printтребует постоянного места, независимо от того, вызываем ли мы ее один или 100 раз.Это означает, что у нас есть постоянная пространственная сложность O (1).Лучший случай, средний случай и худший случай
При вычислении Big O нас интересует только худший случай. Но также может быть важно рассмотреть средний случай и знать лучший случай.
Например, при поиске значения в несортированном массиве в лучшем случае значение будет первым элементом в массиве. Это приведет к O (1). И наоборот, если искомое значение было последним элементом в массиве или не было в массиве, в худшем случае было бы O (n).
def совпадение (lst, совпадение): для элемента в lst: если item == соответствует: вернуть True вернуть ложь lst = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
В лучшем случае: Найдите предмет на первой позиции.
matcher (lst, 1) # O (1) - КонстантаХудший случай: Найти предмет на последней позиции.
matcher (lst, 10) # O (n) - линейныйBig O для структур данных
Связанные списки
По сравнению с массивами, связанные списки требуют больше времени, но меньше места.
Связанные списки экономят память, потому что вы создаете только те элементы, которые вам нужны, нет необходимости заранее создавать массив фиксированного размера для статического массива или справляться с процессом копирования, который поставляется с динамическим массивом.
Обратной стороной является то, что поиск предметов занимает больше времени. Это связано с тем, что при создании узлов они могут не находиться близко друг к другу в памяти. Это означает, что мы не можем выполнить то же вычисление O (1), чтобы определить значение по его индексу, как мы можем с массивом.
В связанных списках при получении элемента 'n' нам нужно пройти список от головы до -го элемента . Следовательно, получение связанного списка имеет временную сложность O (n), которая является линейной.
Та же самая логика применяется для добавления нового элемента в связанный список. Вам нужно перейти от головы к последнему элементу, а затем установить указатель «следующий» последнего элемента в качестве нового узла. Вот почему добавления также считаются временем O (n).
Напротив, добавление элемента в начало связанного списка - это операция с постоянным временем O (1).Нам просто нужно сделать новый узел заголовком связанного списка, направив его на предыдущий головной узел. Количество выполняемых операций не зависит от размера списка.
Единственный способ добавить операцию O (1) - это сохранить ссылку на конечный узел связанного списка. Таким образом вы могли:
- Создайте новый узел
- Установить атрибут 'next' хвостового узла как новый узел
- Установите ссылку "хвост", чтобы указать на ваш новый узел
Хеш-таблицы
Сложность операций с хеш-таблицей во многом зависит от качества хэш-функции.Даже если предположить, что хеш-функция вычисляет хэш ключа за постоянное время O (1), если все значения хешируются в один и тот же слот, и вы используете связанный список для обработки коллизий, результатом будет поиск O (n).
Вставка в хеш-таблицу будет только O (1), если вы используете связанный список для обработки коллизий и поддерживаете указатель на хвост для O (1) добавлений.
Двусвязные списки
Основное преимущество двусвязных списков (DLL) перед односвязными списками (SLL) с точки зрения временной сложности состоит в том, что вы можете использовать их для поиска предыдущего узла в постоянное время.
С SLL, если нам дают узел и говорят найти предыдущий узел, мы должны идти от головы до тех пор, пока не найдем данный узел. В худшем случае это будет O (n).
Каждый узел в DLL содержит указатель на предыдущий узел, поэтому мы можем просто использовать этот указатель для получения значения предыдущего узла за время O (1).
Big O для операций Python
Список операций
Некоторые методы списков выполняют одинаковое количество основных операций независимо от размера списка, поэтому используйте постоянную временную сложность O (1).Для других методов списков количество выполняемых ими операций пропорционально количеству элементов в списке, поэтому используйте линейную временную сложность O (n).
Простой пример:
- O (1): Метод
pop ()всегда удаляет элемент в конце списка. Неважно, насколько велик список, нужно выполнить только одну операцию. - O (n): Метод
remove ()должен заполнить пробел, переместив все элементы справа от того, который был удален.В худшем случае будет удален первый элемент, а это значит, что все элементы в списке необходимо переместить.
Более сложный пример: O (n): метод
append ()добавляет элемент в конец списка. Если память, выделенная для списка, уже была достаточно большой для хранения существующих элементов и нового элемента, то временная сложность была бы постоянной O (1).Однако, если список был заполнен до
append (), вам необходимо выделить новый массив с размером, достаточным для хранения всех существующих элементов, а также элемента, который вы добавляете.Затем Python скопирует все элементы из старого массива в новый массив, сделав временную сложность наихудшего случая пропорциональной размеру списка. Следовательно, операция спискаinsert ()имеет линейную временную сложность O (n).Эксплуатация Пример Big-O Индекс список [0] O (1) Магазин список [0] = 0 O (1) Приложение список.добавить (4) O (1) Поп list.pop () O (1) Прозрачный list.clear () O (1) Длина л. (Список) O (1) Индекс населения list.pop (0) O (n) Удалить list.remove ('x') O (n) Insert list.insert (0, 'a') O (n) Del operator del list O (n) Итерация для v в списке: O (n) Сдерживание 'x' в списке1 O (n) Равенство list1 == list2 O (n) Копия список.копия () O (n) Задний ход list.reverse () O (n) получить фрагмент [x: y] список [a: b] O (k) del slice del list [a: b] O (n) набор срезов O (n + k) объединить O (k) Сортировка list.sort () O (n log n) Умножить 5 * список O (k n) Словарные операции
Эксплуатация Пример Big-O Индекс dict [0] O (1) Сохранить dict [0] = 'значение' O (1) Длина len (dict) O (1) Удалить del dict [0] O (1) Получить дикт.получить (0) O (1) Pop dict.pop () O (1) Pop item dict.poITEm () O (1) Прозрачный Прозрачный () O (1) Просмотр дикт. Клавиши () O (1) Итерация для k в dict: O (n) Защитная оболочка x in dict: O (n) Копия dict.копия () O (n) Установить операции
Наборы содержат больше операций, равных O (1), по сравнению со списками или словарями. Отсутствие необходимости хранить данные в порядке снижает сложность.



